Penjumlahan Matriks (+)
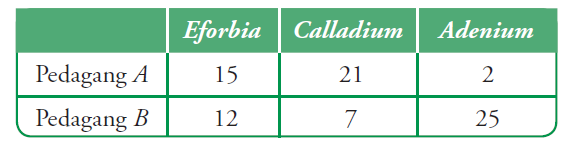
Untuk memudahkan Anda dalam memahami penjumlahan pada matriks, pelajarilah uraian berikut. Di suatu kompleks perumahan terdapat dua kepala keluarga yang bermata pencaharian sebagai seorang fl oris (pedagang tanaman hias). Beberapa tanaman hias yang sering mereka jual di antaranya adalah eforbia, calladium, dan adenium. Berikut ini adalah persediaan tanaman-tanaman tersebut di kedua pedagang tersebut.
Untuk menambah persediaan barang, kedua pedagang tersebut pada hari yang sama melakukan pembelian tanaman-tanaman baru yang jumlahnya disajikan pada tabel berikut.
Kedua tabel pada uraian tersebut jika diubah ke dalam bentuk matriks dan dijumlahkan adalah sebagai berikut.
Berapa banyakkah pesediaan ketiga jenis tanaman yang ada di masingmasing pedagang setelah dilakukan pembelian tersebut? Untuk menjawab pertanyaan sangat mudah bagi Anda untuk mendapatkan jawabannya. Langkah yang dilakukan adalah menjumlahkan banyaknya tanaman pada persediaan awal dengan tanaman yang dibeli sebagai penambahan persediaan. Tentu saja yang dijumlahkan harus sejenis dan pada pedagang yang sama, misalnya banyak tanaman eforbia yang ada di pedagang A dijumlahkan dengan banyaknya tanaman eforbia yang dibeli oleh pedagang A (yang dijumlahkan harus bersesuaian). Kedua tabel tersebut dapat disederhanakan dan diubah ke dalam bentuk matriks. Selanjutnya melakukan pejumlahan matriks, yaitu yang dijumlahkan adalah elemen-elemen yang seletak. Berikut defi nisi dari penjumlahan matriks.
Pengertian Penjumlahan Matriks
Jika A dan B adalah dua matriks yang berordo sama maka jumlah dari matriks A dan B (ditulis A + B) adalah sebuah matriks baru yang diperoleh dengan cara menjumlahkan setiap elemen matriks A dengan elemen-elemen matriks B yang seletak (bersesuaian).
penjumlahan dua matriks berordo 2 x 2 berikut ini.
Penjumlahan Matriks Ordo dua x dua (2 x 2)
maka: A + B = ${\begin{bmatrix} a+e&b+f\\ c+g&d+h \end{bmatrix}}$
Pembahasan Soal Latihan dua matriks ordo 2 x 2:
Soal 1
A + B = $\begin{bmatrix} 4+3& 3+2& 2+1 \\ 1+2& 2+1& 5+4 \\ \end{bmatrix}$
A + B = A + B = $\begin{bmatrix} 7& 5& 3 \\ 3& 3& 9 \\ \end{bmatrix}$
Soal 2
P + Q = $\begin{bmatrix} 1+(-2)& 2+1& (-3)+2 \\ -4+3& -5+4& -6+5 \\ \end{bmatrix}$
P + Q = $\begin{bmatrix}-1& 3& -1 \\ -1& -1& -1 \\ \end{bmatrix}$
Soal 3
A + B + C = $\begin{bmatrix} 2+3+4& 1+2+3& 3+1+2 \\ 4+2+1& 2+5+2& 6+6+3\\ \end{bmatrix}$
A + B +C = $\begin{bmatrix} 9& 6& 6 \\ 7& 9& 15 \\ \end{bmatrix}$
Soal 4
A + B + C = $\begin{bmatrix} 2+3+4& 1+2+3& 3+1+2 \\ 4+2+1& 2+5+2& 6+6+3\\ \end{bmatrix}$
A + B +C = $\begin{bmatrix} 9& 6& 6 \\ 7& 9& 15 \\ \end{bmatrix}$

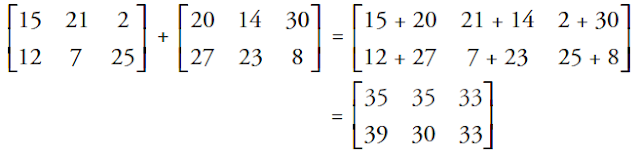
Post a Comment for "Penjumlahan Matriks (+)"